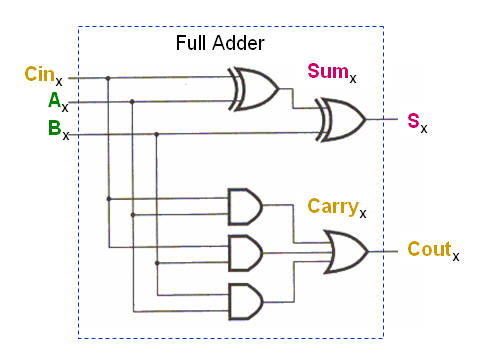
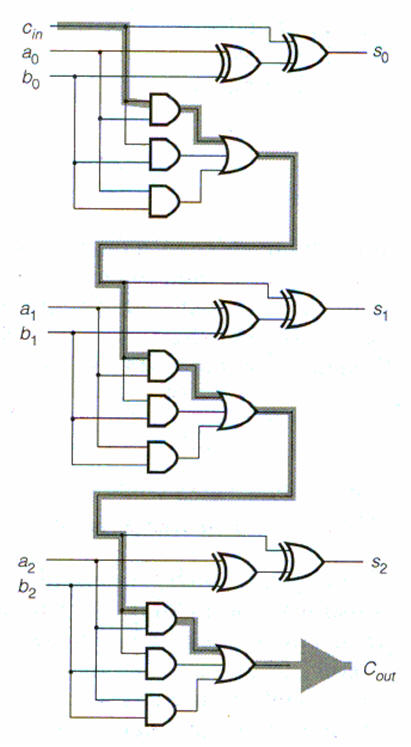
The basic element for most adders called a Full Adder (and can be formed by two Half Adders :-)

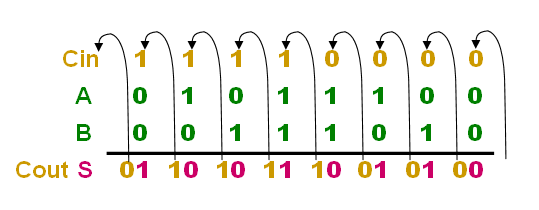
The Full Adder able to "calculate" the sum of 3-bits and hence give results like 0, 1, 2 or 3 (decimal numbers) which 00, 01, 10 or 11 binary.

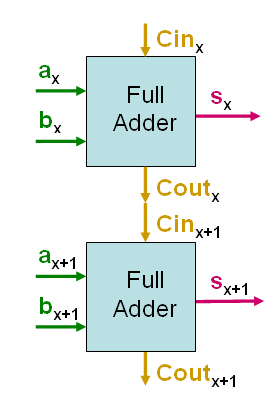
In order to create  adders for N+N-bit addition must you take N Full Adders and connect the in a chain.

The principle will be very much the same when we do the addition by "hand" at a sheet of paper.

 

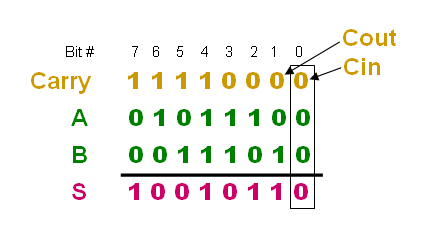The good thing about Ripple Carry adders the relative simple hardware it takes to form a N+N-bit adder.

The bad thing can be found the nature of the Ripple Carry. It cost 2 x Gate delays for each stage formed by a Full Adder.

A 32-bit Adder will then:

Use 128 Gates for the Carry Chain

Have a propagation delay of 64x Tp

 

The "text-book" implementation.

 

Alternative version of the FA which in the end will be implemented the same way as the "Text-book" version above.

 

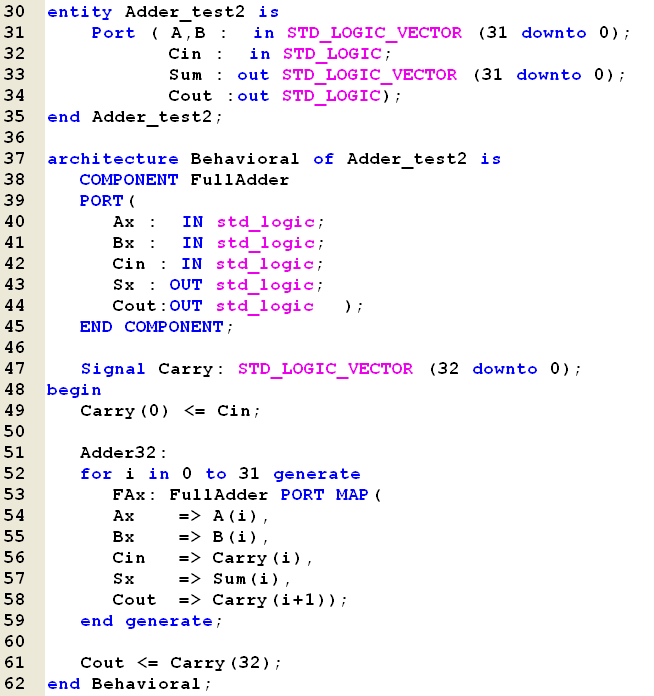
One way of implementation could be a schematic diagram with 32 Full Adders drawn and connected in a chain.

Alternative could a Structured VHDL code be written with the same result - 32 Full Adder connected in a chain.

The most elegant way how ever to use the generate statement of VHDL and an internal Carry Vector with N+1 elements.

Each Full Adder will then take a Carry from Carry(i) and produce the next Carry for Carry(i+1).

The Last element in the Carry chain will in the end be the new Cout value.

 

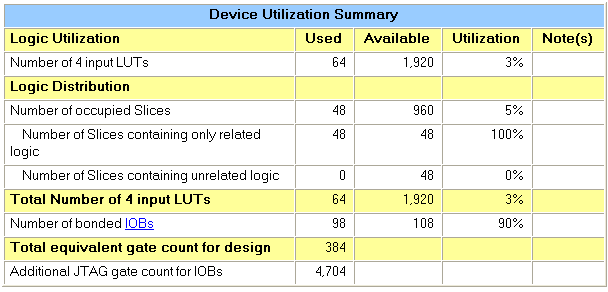
Just as expected will a 32+32-bit adder use 64 LUTs (one LUT for the SUM and one LUT for the Carry in each Full Adder)

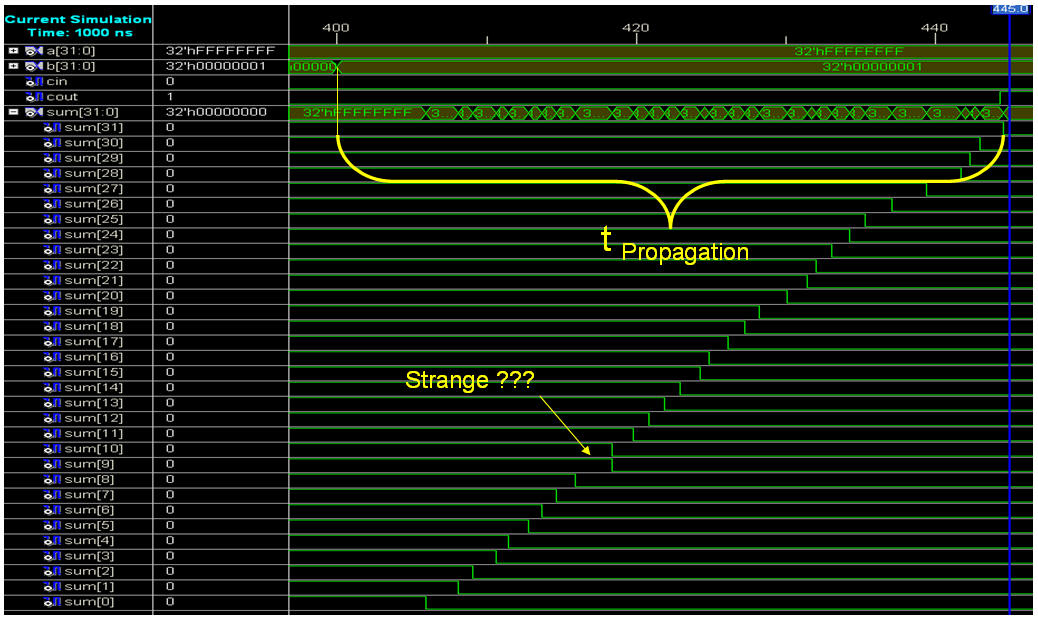
Just as expected will the ripple nature of the Carry be shown in a simulation of the Ripple Carry adder.
Strange result for the Sum(11) and Sum(10) but never mind .....