[Home] [Why ...] [Boolean algebra] [Carnaugh Maps] [AND-OR-NOT] [Number Systems] [Combinatorial logic] [Sequential logic] [State-Machines] [Examples]
 AND-OR-NOT
 [ Up ]

The basic logic functions and equivalent gates

Given a box with two inputs A, B and one output Fx - How many logic functions possible inside the box?

Answer:   Drag the mouse over the box below (hold the left button down)
A B F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15
0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1


There's  16 possible functions but not all that useful and given a name like: AND, NAND, OR, NOR, XOR, XNOR
 
TTL CMOS PAL CPLD FPGA
A F(NOT)
0 1
1 0

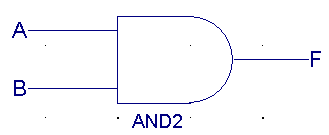
A B F(AND)
0 0 0
0 1 0
1 0 0
1 1 1

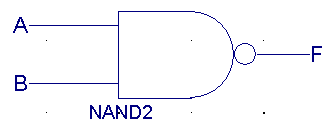
A B F(NAND)
0 0 1
0 1 1
1 0 1
1 1 0

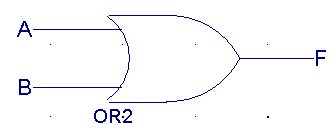
A B F(OR)
0 0 0
0 1 1
1 0 1
1 1 1

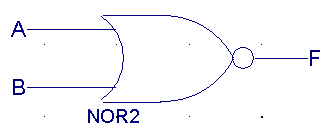
A B F(NOR)
0 0 1
0 1 0
1 0 0
1 1 0

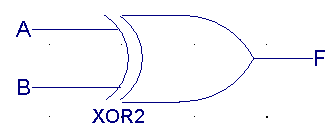
A B F(XOR)
0 0 0
0 1 1
1 0 1
1 1 0

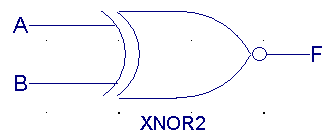
A B F(XNOR)
0 0 1
0 1 0
1 0 0
1 1 1

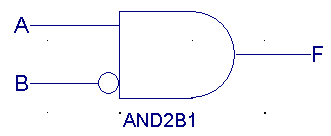
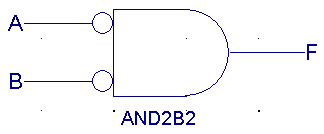
A /B F(ANDb1)
0 1 0
0 0 0
1 1 1
1 0 0
 

/A /B F(NOR)
1 1 1
1 0 0
0 1 0
0 0 0

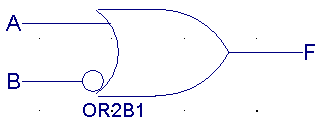
A /B F(ORb1)
0 1 1
0 0 0
1 1 1
1 0 1
 

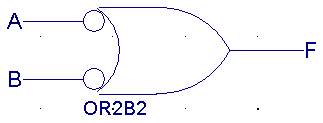
/A /B F(NAND)
1 1 1
1 0 1
0 1 1
0 0 0